C++とJavaでつくるニューラルネットワーク正誤表

■正誤表　（初版1刷）

ページ	誤	正
p.28 8行目	結合荷重をX (上付：n,n-1、下付：i,j)	結合荷重を W (上付：n,n-1、下付：i,j)
p.31 Fig.2-7	X (上付：N、下付：3) ← d(下付：3)	X (上付：N、下付：i) ← d(下付：i)
p.166 Eq.9-12 p.182 Eq.10-6 p.212 Eq.12-4	(1-tanh	(1＋tanh
p.247 Eq.13-5の右辺	vp（t+1）	vp（t）
p.255 14行目	すべての出力層ユニットを対称に	すべての出力層ユニットを対象に
p.272 Fig.15-2 左ボックス一番上	ColorMap	SOMzoo
本文1行目	■□SOMtsp	■□SOMzoo

■正誤表　（初版2刷）

ページ	誤	正
p.31 Fig.2-7	X (上付：N、下付：3) ← d(下付：3)	X (上付：N、下付：i) ← d(下付：i)
p.166 Eq.9-12 p.182 Eq.10-6 p.212 Eq.12-4	(1-tanh	(1＋tanh

■p.166 Eq.9-12の使用について（Eq.8-1の式との関連等）の補足

Eq.8-1 は、状態変化を行う際にステップ関数を用いていて，結果が，0 か 1 と　しています。これは、初期のHopfieldモデルのものです。その後HopfieldとTankは、連続値を取り扱えるように拡張して、組み合わせ最適化問題の解法に応用できることを示しました。
そこで、本書では，最適化問題を解くために連続値の表現を用い、Eq.9-12のような、いわゆるSigmoid(S字)関数を採用することとしました。
tanh(x)をグラフ表示するとFig.2-6(p.30)で示した姿と同じような変化をし、急激な階段状にではなく滑らかに、ステップ変化させることができることは、ご承知のことと思います。このSigmoid関数には、ここで採用した、tanh(...)やEq.2-5 の1/(1+exp(a-x)) といった関数がありますが、いずれも，微分した結果が微分前の関数を使って表現できるという、解析的に扱いやすい性質があるため、この種の関数が採用されています。

■Visual Studio .NET2003/.NET2005への対応情報

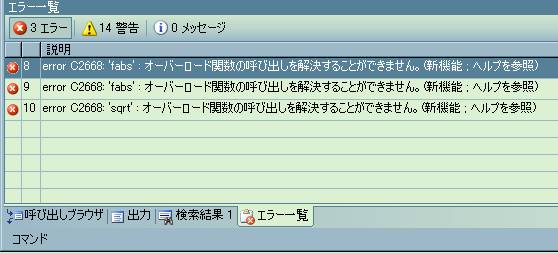
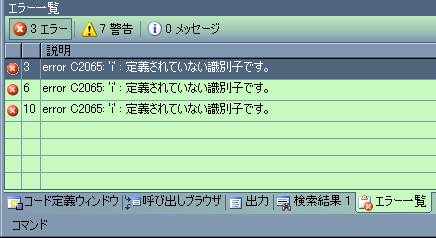
Visual Studio .NET2003/.NET2005において、本書掲載のプログラムでエラーが発生いたします。
これは本書で使用しておりますVC++6.0 と　2003以降の環境の違いによるもので、ライブラリの関数名が微妙に異なっているため起こります。プログラムの変更情報については下記をご参照ください。

Visual Studio .NET2003 への変更
相互結合型相互結合型については、変更ありません。階層型 ■ Count Count.cppの39、40行の定義文の値を以下の数値に変更してください。（Seedは13でよい） #define Eta 0.6 #define Alpha 0.9 自己組織化マップ（SOM） ■ SOMzooとColorMap SelfOrganizingMap.cppのupdateWeight() 関数内について、以下の変更を行います。 8 ： fabs を abs に変える。 9 ：同上 10 ： sqrtの引数に (double) のキャストを行う。 sqrt( dwdw + dhdh );　⇒　sqrt( (double)(dwdw + dhdh) ); ■ SOMtsp ・上記と同じコンパイルエラーは、上と同じ対応となります。・実行して、DrawResultにおける結果の描画時に、エラーが出ます。 DrawResult.cpp の最後の行の下記ステートメントが余分となりますので、これを削除します。 delete cB;

Visual Studio .NET2003 への変更

相互結合型

相互結合型については、変更ありません。

階層型

■ Count

Count.cppの39、40行の定義文の値を以下の数値に変更してください。（Seedは13でよい）

#define Eta 0.6
#define Alpha 0.9

自己組織化マップ（SOM）

■ SOMzooとColorMap

SelfOrganizingMap.cppのupdateWeight() 関数内について、以下の変更を行います。

8 ： fabs を abs に変える。
9 ：同上
10 ： sqrtの引数に (double) のキャストを行う。

sqrt( dw*dw + dh*dh );　⇒　sqrt( (double)(dw*dw + dh*dh) );

■ SOMtsp

・上記と同じコンパイルエラーは、上と同じ対応となります。

・実行して、DrawResultにおける結果の描画時に、エラーが出ます。
DrawResult.cpp の最後の行の下記ステートメントが余分となりますので、これを削除します。

delete cB;

Visual Studio .NET2005 への変更
（注）下記に示す .NET2005への変更は、上記 .NET2003の変更も行う必要があります。
相互結合型相互結合型については、変更ありません。階層型 ■ CpRecog 上記のすべてのコンパイルエラーについての対応は以下となります。ファイル CprChin.h について、下記のように、変数 i の宣言をfor ループの外に出します。 int i; for( i = 0; i < strlen( s ); i++ ) { if ( s[i] == ':' ) break; } strcpy( token,&s[i+1] ); 自己組織化マップ（SOM） .NET2003の変更を参照してください。

Visual Studio .NET2005 への変更

（注）下記に示す .NET2005への変更は、上記 .NET2003の変更も行う必要があります。

相互結合型

相互結合型については、変更ありません。

階層型

■ CpRecog